回路図エディタでボード線図を使用してコンバータ設計の問題をトラブルシューティングする

導入

電気駆動アプリケーションにおいて、整流器は直流電圧オーバーシュートの問題に悩まされる傾向があります。本稿では、図1に示すような制御されていない三相ダイオード整流器を用いて、これらの問題の発生可能性を検証します。入力インピーダンスはボード線図を用いて計算し、モデルに導入することができます。この直流リンク電圧のピークは、三相ダイオード整流器のダイオードや、オーバーシュート電圧の定格を満たしていない三相インバータのIGBTの焼損につながる可能性があります。

モデルの説明

駆動システムの整流器部分のモデルを図1に示します。

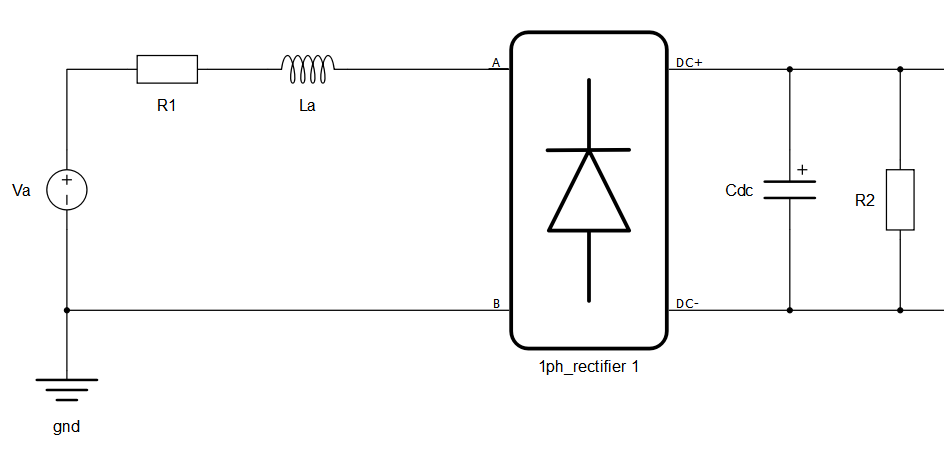
以下のコードブロックのモデル初期化関数を使用することで、Pythonライブラリのscipyとmatplotlibを用いてボード線図を生成できます。scipyライブラリの最も重要な関数は、 scipy.signal.TransferFunctionとscipy.signal.bodeです。

モデル初期化スクリプトを以下に示します。

# Numpy module is imported as 'np'
# Scipy module is imported as 'sp'
import matplotlib.pyplot as plt
          
#parameters that chan be changeable
Rprech = 0
Ts = 100e-6
R = 0.1
L = 0.0011
C = 0.0022
RloadAnalys = 100
          
#Solution no. 1: fix with inductor
#L = C * R**2 *0.9**2
#mdl.info(L)
         
#Solution no. 2: fix with capacitor
#fsw = 100
#C = 1/(2*np.pi*0.3*fsw)**2/L
#mdl.info("C = {} F".format(C))
          
#Solution no. 3: add precharge resistor Q = 0.707
Rprech =np.sqrt(2)*(np.sqrt(L/C)-1/np.sqrt(2)*R)
mdl.info("Rprech = {} ohm".format(Rprech))
          
#bode diagram analysis
# resonant frequecny
f0 = 1/(2*np.pi*np.sqrt(L*C)) 
mdl.info("f0 = {} Hz".format(f0))
w0 = 2*np.pi*f0
          
# absolute Q factor
Qab = 1/(R+Rprech)*np.sqrt(L/C)
mdl.info("Qab = {}".format(Qab)) 
Qdb = 20 * np.log10(Qab)
# Q factor in db         
          
#bode plot using sp.signal.lti function
s1 = sp.signal.lti([1],[1/w0**2,1/(w0*Qab),1])
w, mag, phase = sp.signal.bode(s1)
         
# Bode magnitude plot
#plt.figure()
plt.semilogx(1/(2*np.pi)*w, mag)
# Bode phase plot
plt.figure(1,1)
plt.semilogx(1/(2*np.pi)*w, phase)
plt.show()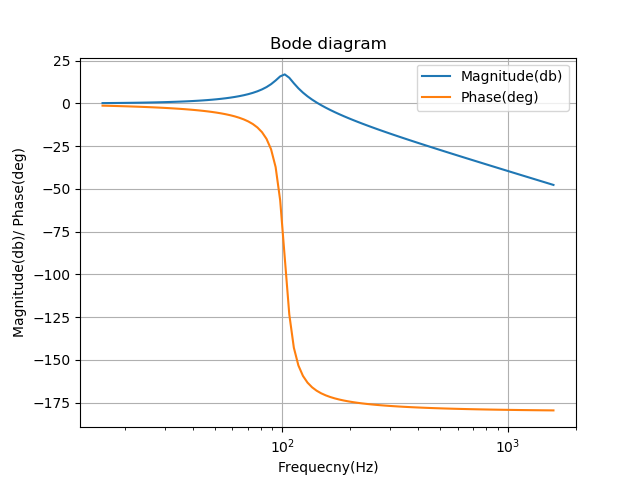        

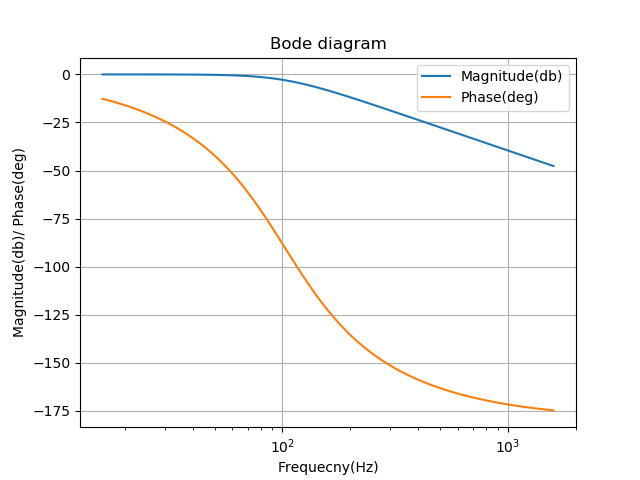
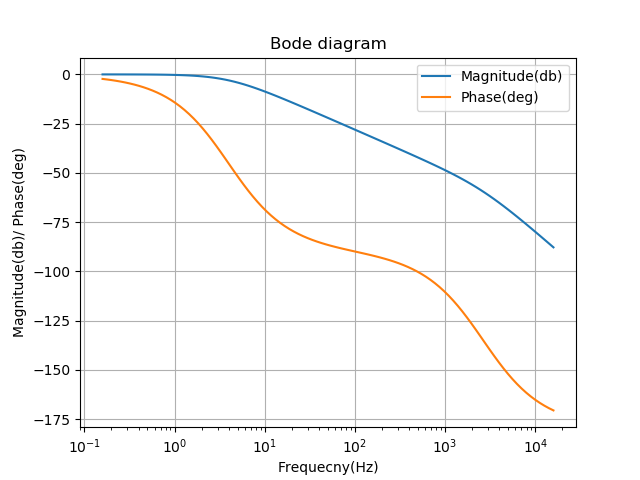
このボード線図と計算から、 $f_0=\frac{1}{2\pi \sqrt{\left(L_{\mathrm{1つの}}{C}_{dc}\right)}}=102.3 Hz$ スイッチング共振周波数とダイオードブリッジのスイッチング周波数（100Hz）がほぼ同じであることがわかります。これは、DC電圧に共振とオーバーシュートが発生することを意味します。ダイオード整流器を使用しているため、スイッチング周波数も変更できません。代わりに、入力インピーダンスのパラメータを変更する必要があります。モデル抵抗（R）を増やすと損失が増加するため、インダクタンス（Q）を下げてインダクタンスに着目する方が適切です。

シミュレーション

このセクションでは、DC リンクの電圧オーバーシュートを解決するための 2 つの解決策として、インダクタンスの低減と静電容量の増加について説明します。

インダクタンスを減少させる問題の解決

まず、入力伝達関数を求めてみましょう。伝達関数は図1の回路から定義されます。

$G_{\left(s\right)}= \frac{1}{1+s{R}_1{C}_{dc}+s^2{L}_{\mathrm{1つの}}{C}_{dc}}$

伝達関数の代替標準正規化形式は次のとおりです。

$G_{\left(s\right)}=\frac{1}{1+\frac{s}{\mathrm{質問}{\omega }_0}+{\left(\frac{s}{{\omega }_0}\right)}^2}$

パラメータQは回路の品質係数と呼ばれ、システムにおける消費電力の尺度です。このパラメータは共振角周波数を表します。

入力伝達関数から、共振周波数は次のようになります。

$f_0=\frac{1}{2\pi \sqrt{\left(L_{\mathrm{1つの}}{C}_{dc}\right)}}$

次の式で Q 係数を簡単に見つけることができます。

$\mathrm{質問}=\frac{1}{R_1}\sqrt{\frac{L_{\mathrm{1つの}}}{C_{dc}}}$

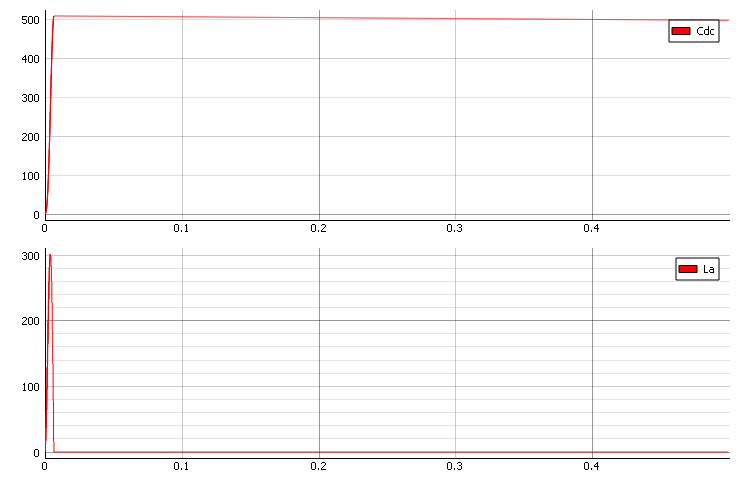
この解析結果から、Q値を下げるためのインダクタの値が分かります。インダクタの値を半分に減らしてみましょう。図4を見ると、DC電圧のオーバーシュートが低減していることがわかります。

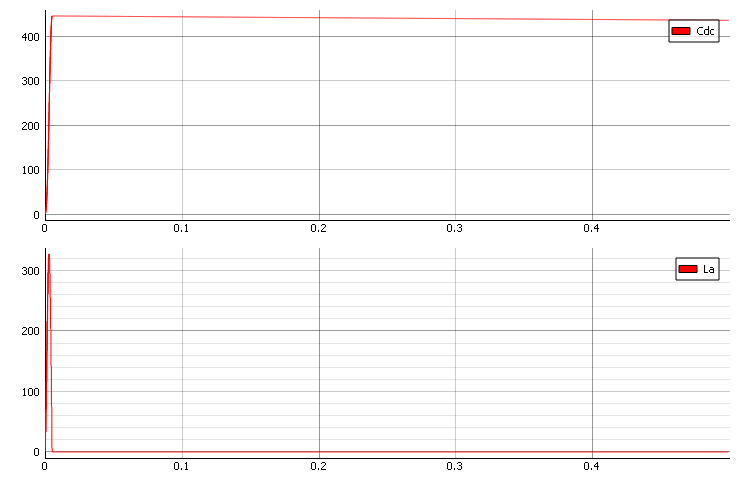
さて、インダクタンスを3分の1に下げてみましょう。図5を見ると、DC電圧（Cdc）を目標の400V以下に下げることができていることがわかります。

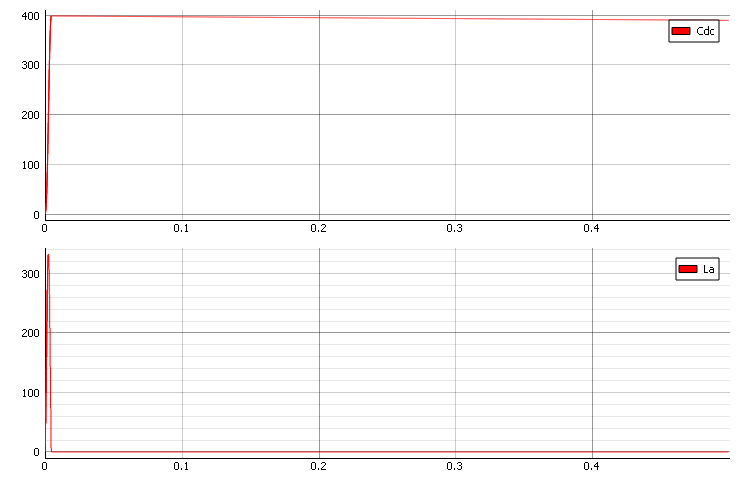
二次的な バターワースフィルタ （つまり、通過帯域周波数応答が最も平坦な連続時間フィルタ）の減衰不足時のQ値は0.707です。したがって、DCコンデンサの電圧のオーバーシュートを低減するには、 Q係数を0.707に設定するさて、インダクタを計算してみましょう。式は次のようになります。 $L_{\mathrm{1つの}c}=C_{dc}{R}_1^2{\mathrm{質問}}^2$ 計算できる場所 $L_{\mathrm{1つの}c}= 1.782e-05$ .

図 6では、この問題を解決できたことがわかります。

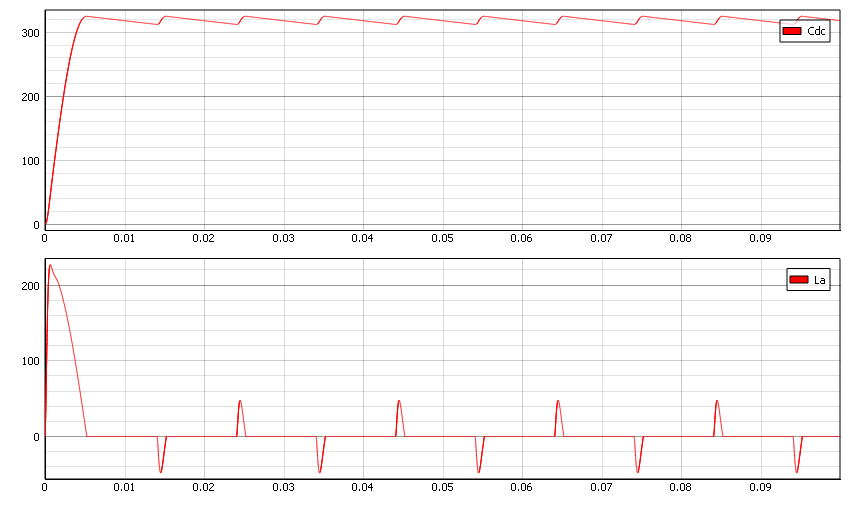
図 7のボード線図では、Q 係数を下げることができることがわかります。

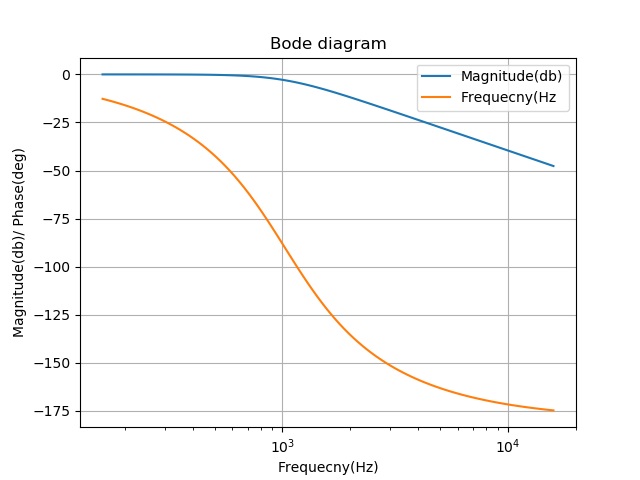
コンデンサを増やすことで問題を解決する

理論的にはインダクタンスを下げれば問題は解決しますが、インダクタはコンデンサよりもはるかに高価なため、現実的ではない場合が多くあります。さらに、モデル内のインダクタンスが電源インダクタンス（つまりグリッドインピーダンス）に起因する場合、それを変更することは不可能です。このような場合、代わりにコンデンサの値を変更することができます。これは、共振周波数をスイッチング周波数から遠ざけることで実現できます。例えば、次のように設定します。 $f_0={0.3f}_{sわ}$ :

$C_{dc}=\frac{1}{{\left(2\pi {0.3f}_{sわ}\right)}^2{L}_{\mathrm{1つの}}}= 0.0255 F$

この新しいコンデンサにより、スイッチング周波数の減衰が得られます。図8に新しいボード線図を示します。

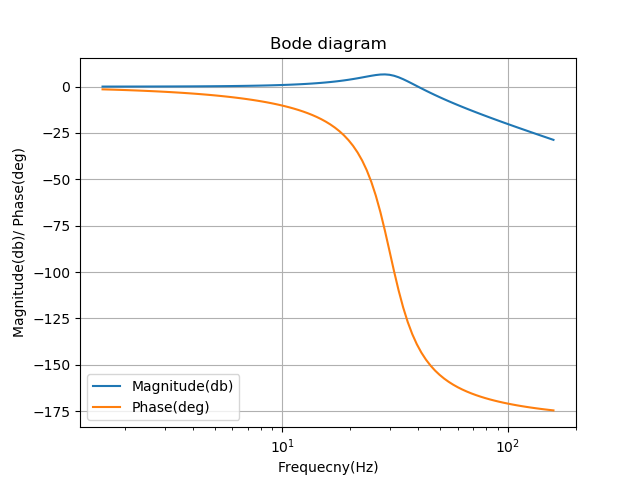
図9では、DCリンクの電圧の新しい応答が確認できます。DCコンデンサを増やすと、インダクタンスを変更したときよりも応答が少し遅くなることがわかります。

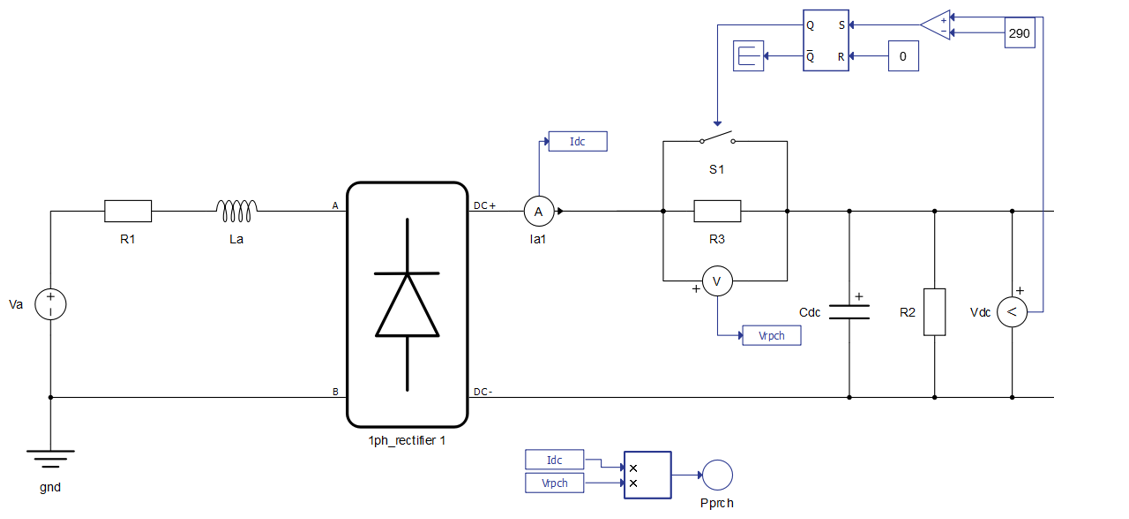
プリチャージ回路

DCリンクの過電圧は、プリチャージ回路によって解決できます。図10に、プリチャージ回路の実装を示します。

この場合、Q係数を設定することでプリチャージ抵抗を計算できます。

$\mathrm{質問}=\frac{1}{\sqrt{2}}$

以下は計算式です $R_{prech}:$

$\mathrm{質問}=\frac{1}{R_1+R_{prech}}\sqrt{\frac{L_{\mathrm{1つの}}}{C_{dc}}}=\frac{1}{\sqrt{2}}$

$R_{prech}= \sqrt{\frac{{\mathrm{2L}}_{\mathrm{1つの}}}{C_{dc}}}-R_1$

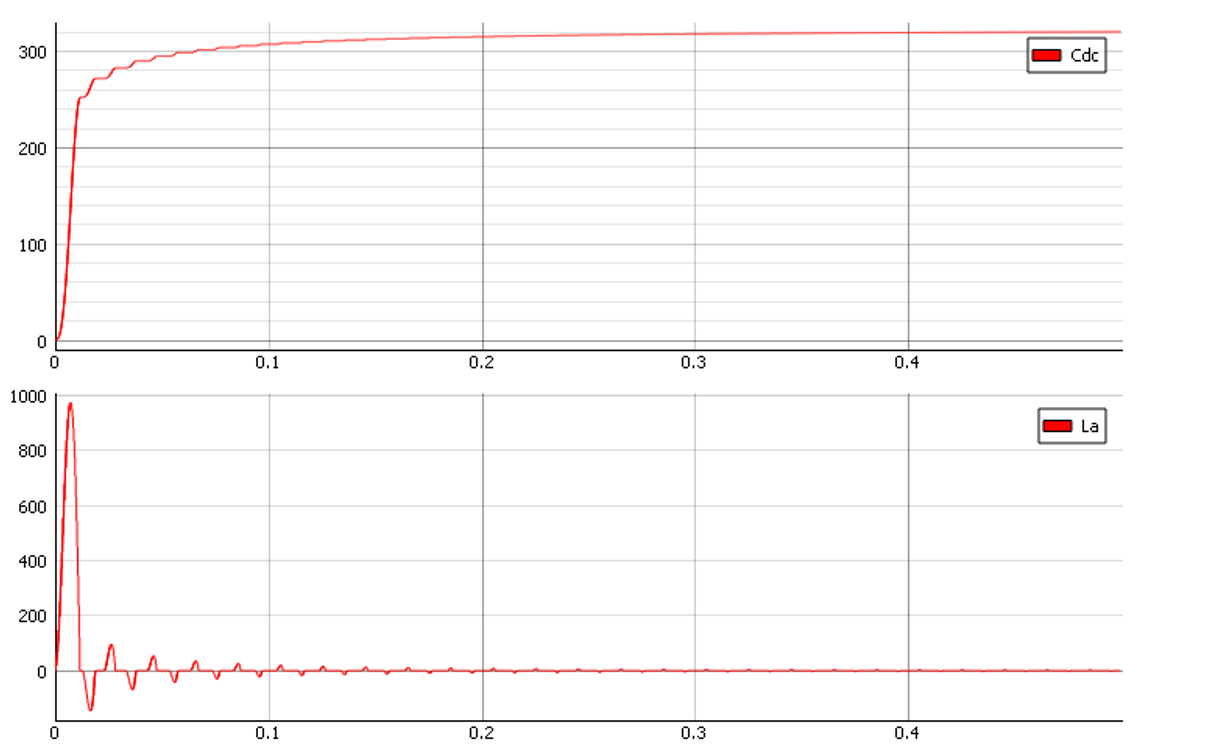
図11は、Q値の低下によって生じるプリチャージ抵抗の影響を示しています。図12は、 DCリンクの電圧応答を示しています。この場合、整流器のAC側への入力電流のピークが減少していることに注目することが重要です。

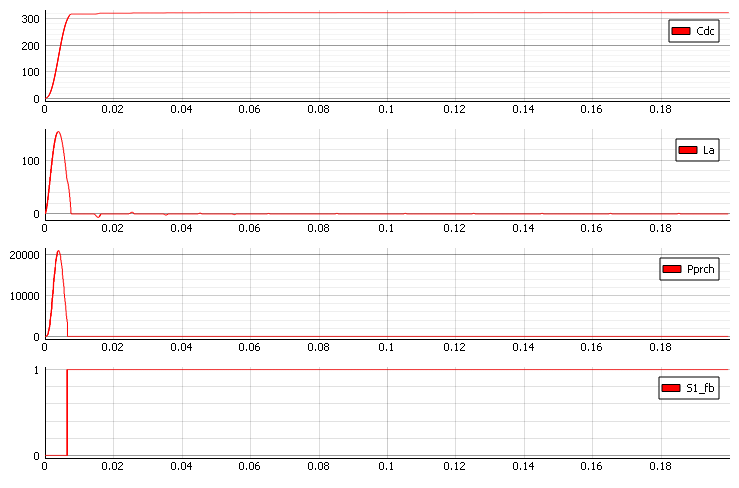
このアプローチを用いることで、パワーエレクトロニクスにおける様々なコンバータやアプリケーションの設計における問題のトラブルシューティングが可能になり、特にDCリンクにおける電圧オーバーシュートを回避できます。図12では、インダクタ電流のピーク値が高いことがわかります。この電流を低減するには、プリチャージ抵抗の値を変更する必要があります。プリチャージ回路の抵抗値は、負荷容量と必要なプリチャージ時間に基づいて選択します。プリチャージサージ電流は、以下の時間後に初期値の1/eに達します。

$T = R_{prech} C$

約 5 * T の時間が経過すると、電流は管理可能な値まで減少します。

$R_{prech}=\frac{T}{5C}$

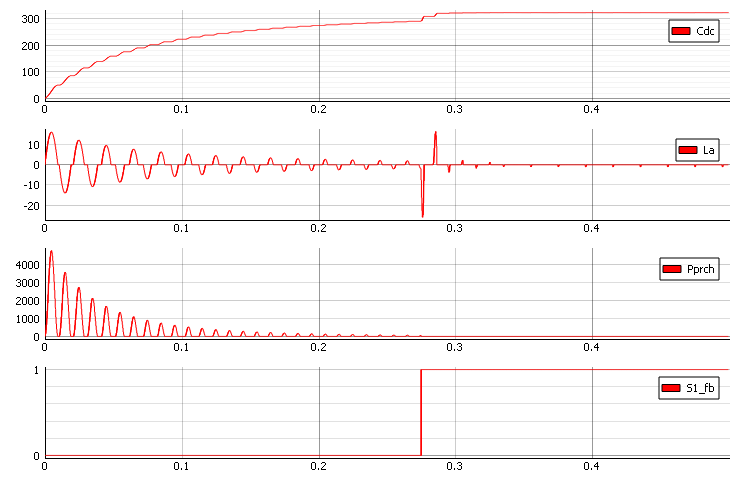
ここで、突入電流をどのように低減できるかがわかります。

実際には、設計が許せば、より大きなコンデンサを配置することで過電圧を解消する選択肢を持つ方が、プリチャージ回路を追加するよりも安価になる可能性があります。これらの結果に基づいて、これを実現する方法を想像することができます。

テスト自動化

この例のテスト自動化はまだありません。ご協力いただける場合はお知らせください。アプリケーションノートへの署名を喜んで承ります。

要件の例

表1は、モデルをリアルタイムで実行するためのファイルの場所とハードウェア要件に関する詳細情報と、この最小限のハードウェア構成でモデルを実行した場合のHILデバイスのリソース使用率を示しています。この情報は、モデルの実行とカスタマイズを必要に応じて行う際に役立ちます。

著者

[1] シミサ・シミッチ