パワーエレクトロニクスデバイスの熱モデリング

パワーエレクトロニクスデバイスの簡略化された熱モデル

パワーエレクトロニクスデバイスの熱モデリングプロセスの最初のステップは、対象となるすべてのコンポーネントの熱挙動を、入力に出力電力、出力にコンポーネント温度を持つ 1 次ローパスフィルタ伝達関数として表すことです。図1 図はモデリングの概念を示しています。熱モデリングの対象となるコンポーネントは、コンバータのヒートシンク (インデックス H で指定)、グリッド電圧トランス (インデックス XFR)、および DC リンク電解コンデンサ (インデックス CAP) です。 $P_{あ V G}$ 1出力電圧周期にわたって平均化された出力電力を示します（インバータの場合 $P_{あ V G}$ 平均皮相電力を表す） $R_{t h_H}$ ヒートシンクと周囲との間の熱抵抗であり、 $C_{t h_H}$ ヒートシンクの熱容量です。 $R_{t h_X F R}$ 変圧器本体と周囲との間の熱抵抗であり、 $C_{t h_X F R}$ 変圧器の熱容量です。 $R_{t h_C あ P}$ コンデンサ本体と周囲との間の熱抵抗であり、 $C_{t h_C あ P}$ コンデンサの熱容量です。 $T_{あ}$ 周囲温度（基準値） $T_{H}$ ヒートシンクの温度は $T_{X F R}$ は変圧器の温度であり、 $T_{C あ P}$ コンデンサの温度です。

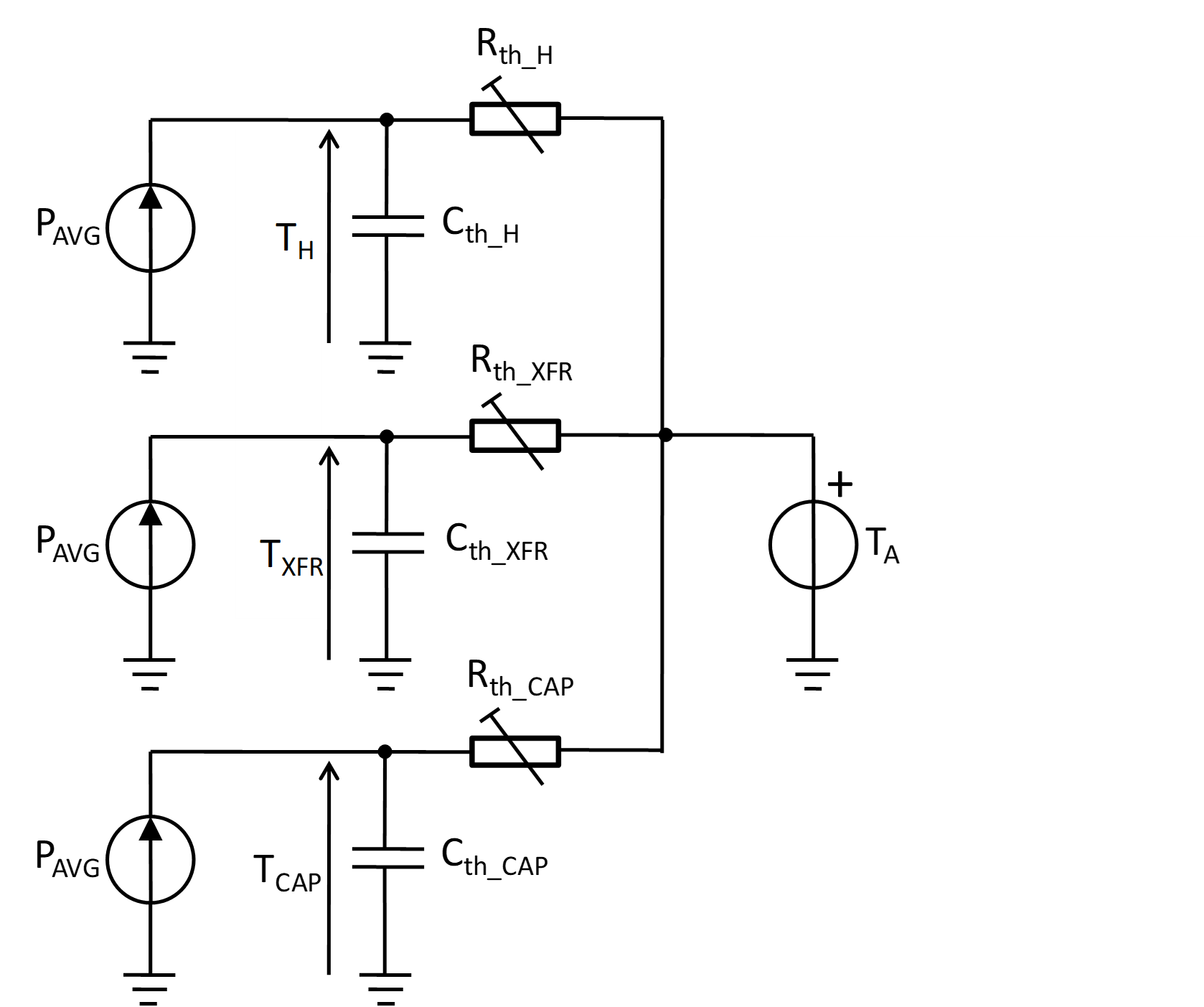
冷却ファンを使用する場合、熱抵抗はファンの速度に依存します。DCモーターでファンを駆動する場合、速度はDCモーターに印加される電圧に正比例します。 $v_{F あ北}$ ファン速度が上昇すると熱抵抗が直線的に低下すると仮定すると、次のように表すことができます。


$R_{t h} = R_{t h_0} + \frac{Δ R_{t h}}{Δ V_{F あ北}} \cdot V_{F あ北}$	(1.1)

モデルの温度の漸近値は次のように表すことができます。


$T_{\infty} = P_{あ V G} \cdot R_{t h} + T_{あ}$	(1.2)

どこ $R_{t h}$ モデルで考慮されるすべての熱抵抗を表す。 $R_{t h_0}$ それらの抵抗の最大値（ファン速度ゼロに相当）であり、 $\frac{Δ R_{t h}}{Δ V_{F あ北}}$ は、温度変化による熱抵抗の変化率である。 $v_{F あ北}$ . $\frac{Δ R_{t h}}{Δ V_{F あ北}}$ 負の数でなければならず、全体の値は $R_{t h}$ 肯定的である必要があります。

モデルのパラメータ、熱抵抗、熱容量は、出力電力のステップ変化後、またはデバイスの電源投入後の各コンポーネントの温度変化を測定することによって決定できます (図 2 )。

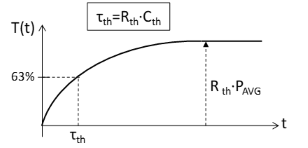
熱時定数 $τ_{t h}$ 部品の熱は、熱抵抗と熱容量の積として定義されます。


$τ_{t h} = R_{t h} ∙ C_{t h}$	(1.3)

これは、平均電力のステップ変化の瞬間からコンポーネントの温度応答が定常状態の 63% に達するまでの経過時間によって求められます。

離散形式の1次ローパスフィルタ

その $R_{t h}$ そして $C_{t h}$ 各熱要素の熱モデル内のセルは、入力が1つのローパスフィルタを形成する。 $P_{あ V G}$ 出力は要素の温度です。離散形式では、ローパスフィルタは次のように表すことができます。図3、どこ $T_{s}$ フィルタのサンプリング周期であり、 $τ_{t h}$ フィルタの時定数です。

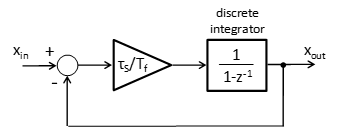
フィルタの伝達関数は次のとおりです。


$X_{o あなた t} = \frac{1}{\frac{τ_{f}}{T_{S}} ∙ (1 - z^{- 1}) + 1} ∙ X_{私 n}$	(1.4)

時間領域では、式（ 1.4 ）は次の形になります。


$\times_{o あなた t} (け) = \frac{1}{1 + \frac{τ_{f}}{T_{S}}} ∙ \times_{私 n} (け) + \frac{\frac{τ_{f}}{T_{S}}}{1 + \frac{τ_{f}}{T_{S}}} ∙ \times_{o あなた t} (け - 1)$	(1.5)

測定 $P_{あ V G}$

平均出力電力、 $P_{あ V G}$ 、（インバータの場合、 $P_{あ V G}$ 平均皮相電力（平均皮相電力を表す）は、電流の基本成分と出力電圧の基本成分に基づいて計算できます。

単相インバータの場合、 $P_{あ V G}$ (皮相電力)は次の式に等しくなります。


$P_{あ V G} = \frac{1}{2} ∙ 私_{メートル 1つの \times} ∙ V_{メートル 1つの \times}$	(1.6)

どこ $私_{メートル 1つの \times}$ 出力電流の基本成分の最大値であり、 $V_{メートル 1つの \times}$ 出力電圧の基本成分の最大値です。

三相インバータの場合、 $P_{あ V G}$ （皮相電力）は次のようになります。


$P_{あ V G} = \frac{3}{2} ∙ 私_{メートル 1つの \times} ∙ V_{メートル 1つの \times}$	(1.7)

どこ $私_{メートル 1つの \times}$ は相電流の基本成分の最大値であり、 $V_{メートル 1つの \times}$ 相電圧の基本成分の最大値です。

の値は $私_{メートル 1つの \times}$ そして $V_{メートル 1つの \times}$ 出力電流と出力電圧の測定サンプルからそれぞれ求める必要があります。電圧源インバータの負荷は誘導性であるため、通常は電流リップルは小さく、 $私_{メートル 1つの \times}$ 得られたサンプルから直接読み取ることができます。

一方、 $V_{メートル 1つの \times}$ サンプリングされた値の処理には、より多くの処理が必要になります。しかし、系統接続されたインバータでは、インバータの出力電圧の基本波は、対応する系統電圧とわずかにしか変わりません。したがって、 $V_{メートル 1つの \times}$ グリッド電圧の測定値から直接見つけることもできますし、グリッド電圧が一定であると想定される場合はパラメータとして入力することもできます。

表1 .簡略化された熱モデルの入力、出力、パラメータのリスト
入力	ユニット	説明
P_平均	W	平均出力（皮相）電力
V_ファン	V	DCモーター電圧駆動ファン
出力	ユニット	説明
T _H	℃	ヒートシンク温度
T _XFR	℃	グリッド変圧器の温度
T_キャップ	℃	DCリンク温度
パラメータ	ユニット	説明
T _A	℃	周囲温度
R _{th_H_0}	℃/W	ファン速度ゼロ時のヒートシンク対周囲温度熱抵抗（V _FAN =0）
R _{th_XFR_0}	℃/W	ファン速度ゼロ時のトランス対周囲温度熱抵抗（V _FAN =0）
R _{th_CAP_0}	℃/W	ファン速度ゼロ時のコンデンサ対周囲温度熱抵抗（V _FAN =0）
R _{th_H} /∆V_ファン	℃/W	V _FANの変化によるヒートシンク対周囲熱抵抗の変化率
R _{th_XFR} /∆V_ファン	℃/W	V _FANの変化による変圧器と周囲間の熱抵抗の変化率
R _{th_CAP} /∆V_ファン	℃/W	V _FANの変化によるコンデンサ対周囲温度熱抵抗の変化率
τ _{th_H}	s∙W/˚C	ヒートシンクの熱時定数
τ _{th_XFR}	s∙W/˚C	グリッドトランスの熱時定数
τ _{th_CAP}	s∙W/˚C	DCリンクコンデンサの熱時定数

損失計算の原則

この文書で示されている損失計算方法は、電力エレクトロニクススイッチングコンポーネントの2大メーカーであるABB[1]とセミミクロン[2これは、1周期にわたる導通損失とスイッチング損失の平均計算に基づいています。 $T_{0}$ 出力周波数の。このアプローチは、自然サンプリングのパルス幅変調（PWM）と正弦波出力電流を使用する単相または三相電圧源インバータに適用できます。したがって、系統接続アプリケーションやモータ駆動アプリケーションにも完全に適用可能です。パワーエレクトロニクス（PE）コンポーネントに必要なデータは、それぞれのデータシートから取得します。

IGBT/MOSFET損失計算の考慮事項

注：このドキュメントはIGBTの損失計算について言及しています。MOSFETに対応するすべての指定インデックスを置き換える限り、すべての考慮事項と計算はMOSFETにも適用できます。

IGBT内部の瞬間損失、 $p_{私 G B T}$ は伝導損失から成り、 $p_{c o n d 私 G B T}$ 、スイッチング損失、 $p_{s わ私 G B T}$ 伝導損失は次のように表されます。


$p_{c o n d 私 G B T} = (V_{C E 0} + r_{C E} ∙ 私_{C}) ∙ 私_{C}$	(2.1)

どこ $V_{C E 0}$ コレクタ・エミッタ閾値電圧、 $r_{C E}$ IGBTのオン状態スロープ抵抗であり、 $私_{c}$ はコレクタ電流である。各IGBT（図4）期間の半分以上を実施 $T_{0}$ (図5）、伝導損失の平均値、 $p_{c o n d 私 G B T}$ は次のように計算できます。


$P_{c o n d 私 G B T} = \frac{1}{T_{0}} \int_{0}^{T_{0} / 2} (V_{C E 0} ∙ 私_{メートル 1つの \times} ∙ s 私 n (ω t) + r_{C E} ∙ {(私_{メートル 1つの \times} ∙ 罪 (ω t))}^{2} ∙ τ (t) ∙ d t$	(2.2)

どこ $私_{メートル 1つの \times}$ は出力電流の最大値であり、τ(t)はパルスパターンの関数である（ $τ = 1$ IGBTがオンになると、 $τ = 0$ IGBTがオフのとき）。出力電流の周期的な形状と $τ (t)$ 、表現（2.2) はインバーター内のすべてのトランジスタに有効です。

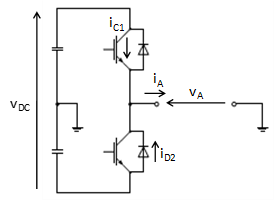
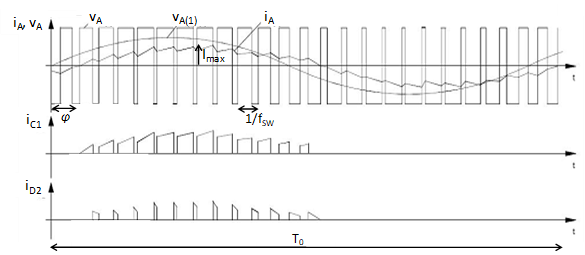
スイッチング周波数を仮定すると、 $f_{s わ}$ は、 $1 / T_{0}$ , $τ (t)$ 次のように近似できます。


$τ (t) = \frac{1}{2} (1 + M ∙ s 私 n (ω t + φ))$	(2.3)

where M is the maximal value of the modulation index (0<M<1 in the linear mode of PWM) and φ is the output current to output the voltage phase displacement angle. By inserting (2.3）の中へ（2.2）を解いて積分を解くと、 $p_{c o n d 私 G B T}$ は、[1], [2]:


$P_{c o n d 私 G B T} = \frac{1}{2} ∙ (V_{C E 0} ∙ \frac{私_{メートル 1つの \times}}{π} + r_{C E} ∙ \frac{私_{メートル 1つの \times}^{2}}{4}) + M ∙ c o s φ ∙ (V_{C E 0} ∙ \frac{私_{メートル 1つの \times}}{8} + \frac{1}{3 ∙ π} ∙ r_{C E} ∙ 私_{メートル 1つの \times}^{2})$	(2.4)

系統接続されたアプリケーションでは、Mは定数とみなされ、損失計算アルゴリズムのパラメータとして入力されます。cosφについても同様です。制御アルゴリズムでは通常、Mは事前設定された値（例えば配電網の場合はcosφ=1）に保持され、パラメータとして入力されます。したがって、 $p_{c o n d 私 G B T}$ , $私_{メートル 1つの \times}$ 測定する必要があります。

IGBTの各スイッチングサイクルにおけるスイッチング損失は、ターンオン損失とターンオフ損失で構成されます。これらは通常、エネルギーの形で表されます。


$E_{s わ私 G B T} = E_{o n} + E_{o f f}$	(2.5)

データシートには損失スイッチングエネルギーの依存性が記載されており、 $E_{s わ私 G B T}$ 、IGBT電流の多項式形式（下の図を参照):


$E_{s わ私 G B T} = {1つの}_{私 G B T} + b_{私 G B T} ∙ 私_{C} + c_{私 G B T} ∙ 私_{C}^{2}$	(2.6)

図6 。曲線の $E_{o n}$ そして $E_{o f f}$ IGBTのスイッチングエネルギーは電流の関数として（誘導負荷スイッチの場合）そして多項式関数近似値として表される。 $E_{s わ私 G B T} (= E_{o n} + E_{o f f})$ [1]

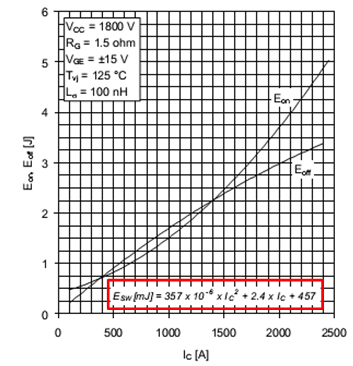
表現（2.6）は、DCリンクに公称値のIGBT電圧が供給されているときに有効です。 $V_{n o メートル}$ アプリケーションでDC電圧が $V_{n o メートル}$ 良い目安としては、カタログ値を比例的に変更することです。 $E_{s わ私 G B T}$ [1]:


$E_{s わ私 G B T} = ({1つの}_{私 G B T} + b_{私 G B T} ∙ 私_{C} + c_{私 G B T} ∙ 私_{C}^{2}) ∙ \frac{v_{D C}}{V_{n o メートル}}$	(2.7)

スイッチング損失の平均値、 $P_{s わ私 G B T}$ 、ある期間中 $T_{0}$ は：


$P_{s わ私 G B T} = \frac{1}{T_{0}} ∙ \sum_{n} E_{s わ} (私_{C})$	(2.8)

ここでnはスイッチングサイクル数を表し、 $1 / f_{s わ}$ 、1つの $T_{0}$ 周期。（2.8）、すなわち（2.7）の表現は $P_{s わ私 G B T}$ は、[1]:


$P_{s わ私 G B T} = \frac{1}{T_{0}} ∙ \sum_{n} E_{s わ} (私_{C})$	(2.9)

スイッチング周波数、 $f s わ$ は、PEコンバータごとに固定されていることが多く、損失計算アルゴリズムのパラメータとして入力することができます。前述のように、多項式係数は、 ${1つの}_{私 G B T}$ , $b_{私 G B T}$ 、そして $c_{私 G B T}$ 、および公称IGBT電圧 $V_{n o メートル}$ これらはすべてデータシートの値です。したがって、 $P_{s わ私 G B T}$ , $私_{メートル 1つの \times}$ そして $v_{D C}$ 測定する必要がある。IGBT損失の平均値、 $P_{私 G B T}$ は、式（2.4）そして（2.9):


$P_{私 G B T} = P_{c o n d 私 G B T} + P_{s わ私 G B T}$	(2.10)

ダイオード損失もほぼ同じ方法で計算されます。平均ダイオード導通損失を導出する過程で、 $P_{c o n d D 私お D E}$ 、パルスパターンτ(t)は、（2.2）（図5）。 $P_{c o n d D 私お D E}$ は次の形式で得られます。


$P_{c o n d D 私お D E} = \frac{1}{2} ∙ (V_{F 0} ∙ \frac{私_{メートル 1つの \times}}{π} + r_{F} ∙ \frac{私_{メートル 1つの \times}^{2}}{4}) - M ∙ c o s φ ∙ (V_{F 0} ∙ \frac{私_{メートル 1つの \times}}{8} + \frac{1}{3 ∙ π} ∙ r_{F} ∙ 私_{メートル 1つの \times}^{2})$	(2.11)

どこ $V_{F 0}$ ダイオードの順方向閾値電圧であり、 $r_{F}$ はダイオードの順方向抵抗です。ダイオードのターンオン時のエネルギー損失は無視できます。ターンオフ時のエネルギーは逆回復エネルギーで表されます。 $E_{r e c}$ は、順方向電流の関数として多項式形式で利用可能である。 $私_{F}$ (下の図を参照):


$E_{r e c D 私お D E} = {1つの}_{D 私お D E} + b_{D 私お D E} ∙ 私_{F} + c_{D 私お D E} ∙ 私_{F}^{2}$	(2.12)

図7 .ダイオードの逆回復パラメータの曲線は、順方向電流（誘導負荷の場合）の関数として、また多項式関数は近似しています。 $E_{r e c}$ ( $私_{F}$ ） [1]

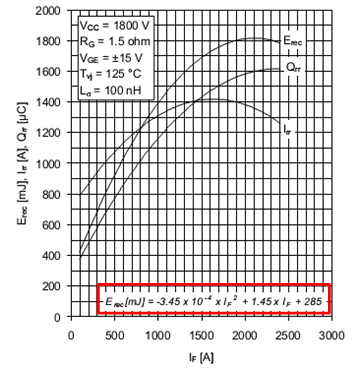
平均回復損失は出力電流の最大値の関数として得られる。 $私_{メートル 1つの \times}$ 、DCリンク電圧、 $v_{D C}$ スイッチング周波数は、 $f_{s わ}$ はパラメータとしてみなされます:


$P_{r e c D 私お D E} = f_{s わ} ∙ (\frac{{1つの}_{D 私お D E}}{2} + \frac{b_{D 私お D E} ∙ 私_{メートル 1つの \times}}{π} + \frac{c_{D 私お D E} ∙ 私_{メートル 1つの \times}^{2}}{4}) ∙ \frac{v_{D C}}{V_{n o メートル}}$	(2.13)

ダイオード損失の平均値、 $P_{D 私お D E}$ は、式（2.11）そして（2.13):


$P_{D 私お D E} = P_{c o n d D 私お D E} + P_{r e c D 私お D E}$	(2.14)

PESBの熱分析

PESBの熱モデルは、次の電気回路と類似した回路で表すことができます。図8ベースプレート付きのPESB、または図9ベースプレートのないPESBに相当する[1熱モデルはIGBTやダイオードの接合温度を計算するためによく利用されます。 $T_{J 私 G B T}$ そして $T_{J D 私お D E}$ 様々な動作条件において、あるいは接合部温度が最大許容値を超えないPESB負荷の最大許容値を求めるために用いられる。モデルでは、電流源の値はIGBTの電力損失に対応する。 $P_{私 G B T}$ 、ダイオード、 $P_{D 私お D E}$ 前のセクションで決定したとおりです。インバータ内の全てのIGBTの平均損失は、ダイオードの平均損失と同様に等しくなります。


$P_{私 G B T (1)} = P_{私 G B T (n)}$ , $P_{D 私お D E (1)} = P_{D 私お D E (n)}$	(3.1)

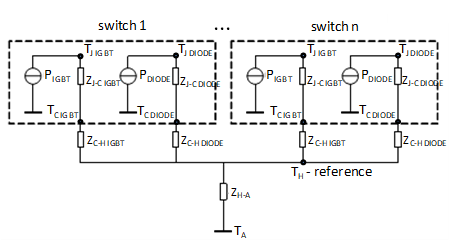
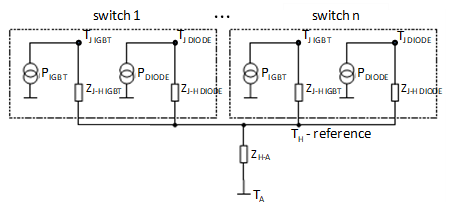
モデルのパラメータには、接合部からケースまでの熱インピーダンス、 $Z_{J - C 私 G B T}$ そして $Z_{J - C D 私お D E}$ 、ケースからヒートシンクまで、 $Z_{C - H 私 G B T}$ そして $Z_{C - H D 私お D E}$ 、周囲へのヒートシンク、 $Z_{H - あ}$ （PESB全体に共通のヒートシンクが想定される）、および周囲温度、 $T_{あ}$ 熱インピーダンスはそれぞれ、熱抵抗と熱時定数という2つのパラメータで構成されます。


$Z_{J - C 私 G B T} = R_{J - C 私 G B T} ∙ (1 - e^{- \frac{t}{τ_{J - C 私 G B T}}})$ , $Z_{J - C D 私お D E} = R_{J - C D 私お D E} ∙ (1 - e^{- \frac{t}{τ_{J - C D 私お D E}}})$ , $Z_{C - H 私 G B T} = R_{C - H 私 G B T} ∙ (1 - e^{- \frac{t}{τ_{C - H 私 G B T}}})$ , $Z_{C - H D 私お D E} = R_{C - H D 私お D E} ∙ (1 - e^{- \frac{t}{τ_{C - D D 私お D E}}})$ , $Z_{H - あ} = R_{H - あ} ∙ (1 - e^{- \frac{t}{τ_{H - あ}}})$	(3.2)

ベースプレートのないPESBモデルには、別途 $Z_{J - C 私 G B T}$ そして $Z_{C - H 私 G B T}$ 接合部がヒートシンク上に直接配置されているため、熱インピーダンスは2つ（ダイオードの場合も同様）となる。代わりに、ヒートシンクに対して2つの熱インピーダンス接合部が存在することになる。 $Z_{J - H 私 G B T}$ そして $Z_{J - H D 私お D E}$ .

熱インピーダンスは、電力損失の伝播に対する一次ローパスフィルタを表します。したがって、対応する伝達関数で表すことができます。例えば、 $Z_{J - C 私 G B T}$ :


$Z_{J - C 私 G B T} (s) = \frac{R_{J - C 私 G B T}}{1 + s ∙ τ_{J - C 私 G B T}}$	(3.3)

ヒートシンクの時定数は、 $τ_{H - あ}$ は、モデル内の他の時間定数、ヒートシンク温度よりもはるかに高い。 $T_{H}$ は、参考値として考えることができる。図8 または図9次のように計算できます。


$T_{H} = n ∙ (P_{私 G B T} + P_{D 私お D E}) ∙ \frac{R_{H - あ}}{1 + s ∙ τ_{H - あ}} + T_{あ}$	(3.4)

ここで、nはPESB内のIGBT/ダイオードペアの数です。最後に、ベースプレート付きモデルでは、IGBTの接合温度は次のようになります。


$T_{J 私 G B T} = P_{私 G B T} ∙ \frac{R_{J - C 私 G B T}}{1 + s ∙ τ_{J - C 私 G B T}} + P_{私 G B T} ∙ \frac{R_{C - H 私 G B T}}{1 + s ∙ τ_{C - H 私 G B T}} + T_{H}$	(3.5)

ダイオードの接合温度は次のようになります。


$T_{J D 私お D E} = P_{D 私お D E} ∙ \frac{R_{J - C D 私お D E}}{1 + s ∙ τ_{J - C D 私お D E}} + P_{D 私お D E} ∙ \frac{R_{C - H D 私お D E}}{1 + s ∙ τ_{C - H D 私お D E}} + T_{H}$	(3.6)

ベースプレートのないモデルでは、同じ式（3.5）そして（3.6）が使用でき、2番目の粒子はゼロ値を割り当てることでキャンセルされます。 $R_{C - H 私 G B T}$ そして $R_{C - H D 私お D E}$ .

DCリンクコンデンサの損失計算と熱モデル

DCリンクコンデンサの損失、 $P_{C}$ はコンデンサ電流のRMS値の2乗に等しい。 $私_{C (R M S)}^{2}$ これにコンデンサの等価直列抵抗を掛けると、 $R_{E S R}$ :


$P_{C} = R_{E S R} ∙ 私_{C (R M S)}^{2}$	(4.1)

DCリンクコンデンサの損失は、適用されるPEコンバータの変調方式によって異なります。したがって、損失計算手順はコンバータの損失計算と連動しています。

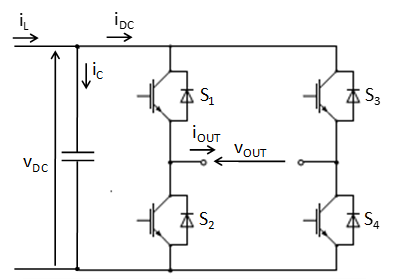
単相インバータDCリンクコンデンサ損失

単相インバータは通常、バイポーラPWMまたはユニポーラPWMのいずれかのPWM方式で制御されます。どちらの方式を選択するかによって、コンバータがDCリンクから引き出す電流が変わります。 $私_{D C}$ .

参考文献

[1] ABB：「 IGBTの適用」、アプリケーションノート、文書番号5SYA2053-04 2012年5月

[2] セミクロン：「アプリケーションマニュアル - パワーモジュール」、初版、セミクロンインターナショナル、2000年、ISBN 3-932633-46-6