機械

機械部品の実装

すべての電気機械コンポーネントは、次の 2 つの部分で構成されています。

電気回路インターフェース
機械ソルバー

回路インターフェースで測定された信号は、機械ソルバーへの入力として使用されます。機械ソルバーはモデル出力を計算し、回路インターフェース内の制御対象ソースに供給します。

回路インターフェース

Typhoon HIL Schematic Editor Library の機械コンポーネントは、電流源インターフェースと電圧リアクタンスインターフェース（ VBR ）の2種類の回路インターフェースを使用します。電流源インターフェースを使用する場合、機械モデル方程式は、電圧が入力、電流が出力となるように定式化されます。逆に、電圧リアクタンスインターフェースを使用する場合、機械モデル方程式は、電流が入力、電圧が出力となるように定式化されます。固定子、回転子、界磁巻線変数は、 HIL SCADA （Typhoon HIL Control Center バージョン 2021.3 以降）およびTyphoonSim Scopeで、 machine_name.winding.variable_nameとして参照できます。

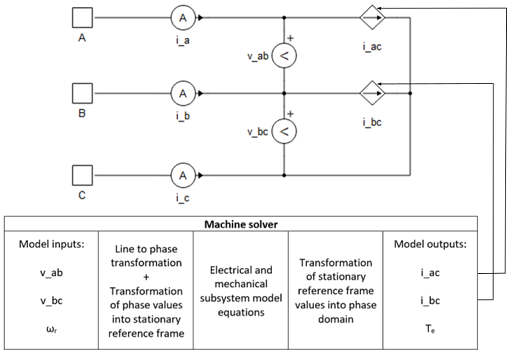
現在のソース実装変数:

v_ab
- 端子AとB間の測定線間電圧[V]
v_bc
- 端子BとC間の測定線間電圧[V]
ω _r
- ローターの機械速度 [rad/s]
i_ac
- 計算されたA相電流[A]
i_bc
- 計算されたB相電流[A]
T _e
- 機械発生電磁トルク[Nm]

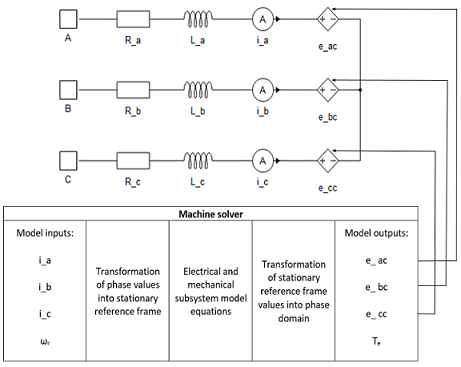
リアクタンス実装変数の後ろの電圧:

i_a
- 測定されたA相電流[A]
i_b
- 測定されたB相電流[A]
IC
- 測定されたC相電流[A]
ω _r
- ローターの機械速度 [rad/s]
e_ac
- 計算されたA相誘導逆起電力[V]
e_bc
- 計算されたB相誘導逆起電力[V]
e_cc
- 計算されたC相誘導逆起電力[V]
T _e
- 機械発生電磁トルク[Nm]

リアルタイム/VHILの機械ソルバー

リアルタイム/VHIL マシンソルバーは、マシンモデルの電気部分と機械部分、およびエンコーダとレゾルバのフィードバック信号をシミュレートする専用モジュールです。電気サブシステムモデル方程式は、マシンの電気的変数を計算するために使用されます。運動方程式とマシンの電気トルク式は、マシンの機械的変数を計算するために使用されます。磁束飽和や空間高調波などの非線形効果は、ルックアップテーブルとしてモデル化されます。単一のマシンコンポーネントで使用されるルックアップテーブルに使用できるポイントの数は 2 ¹⁵です。ルックアップテーブルで提供されるポイントの合計数がこの数を超えると、テーブルはより少ないポイントで動作するように再スケールされます。結果として得られるテーブルの解像度は、元のテーブルよりも低くなる可能性があります。ルックアップテーブルでは、線形内挿と線形外挿が使用されます。非線形マシンツールボックスの詳細については、ここを参照してください。

TyphoonSimの機械ソルバー

TyphoonSimの機械モデルは、制御電流源またはリアクタンス背後電圧（VBR）インターフェースを使用して実装されます。どちらの実装でも、相電圧と相電流は各時間ステップでサンプリングされ、機械の状態空間モデルを解くために使用されます。

機械モデルでは現在、メインソルバーとは別に、小さな時間ステップで安定した結果を得るのに適した、陽的一次オイラー積分法を使用しています。今後のアップデートでは、より洗練された機械モデル用積分法の提供が予定されています。

電流源インターフェースを備えた機械の場合、相電圧はモデルと機械ステータへの入力としてサンプリングされ、（回転子回路が存在する場合）回転子磁束または電流が状態変数として選択されます。その後、機械電流はαβ0座標またはdq0座標のいずれかで機械数学モデルに従って計算され、位相領域に変換されて電流源に適用されます。

リアクタンス背後電圧（VBR）実装において、機械に回転子回路がある場合、回転子磁束が状態変数として選択され、固定子電流が状態空間モデルへの入力として使用されます。この状態空間モデルは、機械の回転子を、等価インダクタに直列に接続され、さらにαβ0座標またはqd0座標で固定子等価回路に接続された制御電圧源として表すために使用されます。VBR構成は、位相座標で回路の残りの部分とインターフェースされます。相電圧は、機械に突極性がある場合、または飽和などの非線形特性がモデル化されている場合にのみ、定数パラメータ（RおよびL）インターフェースを取得するために必要な計算を行うための入力として使用されます。

参照フレーム

参照フレーム変換は、機械モデル内の時間変動インダクタンスを除去するために一般的に使用されます。特に明記されていない限り、Typhoon HIL Schematic Editor ライブラリ内のすべての機械モデルは、以下のいずれかの参照フレームを使用して実装されています。

静止したαβ参照フレーム
回転dq参照フレーム

静止したαβ参照フレーム

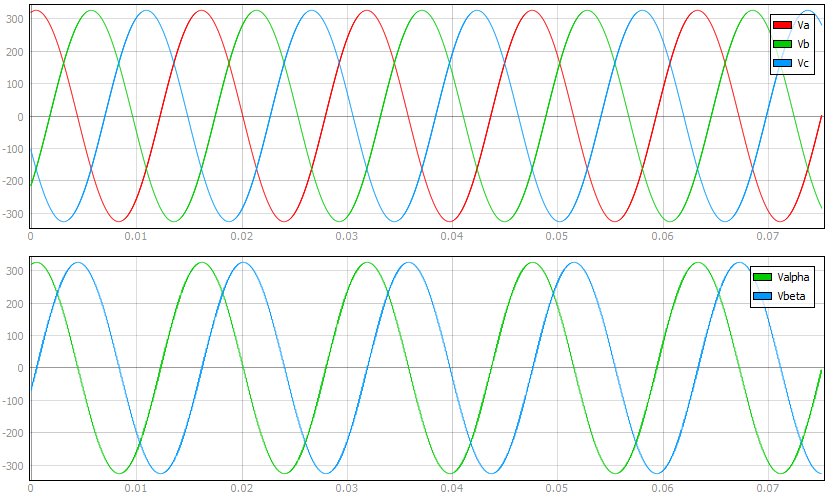
クラーク変換は、固定子と回転子の電気変数を元の 3 相領域から定常 2 相 αβ 領域に変換します。

電気変数は変換行列を使用してαβ成分に変換されます。

$T_{ABC / αβo} = \frac{2}{3} [\begin{matrix} c o s θ_{1つの b} & c o s (θ_{1つの b} - \frac{2 π}{3}) & c o s (θ_{1つの b} + \frac{2 π}{3}) \\ - s 私 n θ_{1つの b} & - s 私 n (θ_{1つの b} - \frac{2 π}{3}) & - s 私 n (θ_{1つの b} + \frac{2 π}{3}) \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{matrix}]$

元の位相領域と同じ電気変数の振幅を維持するために、abc/αβ変換行列に2/3の乗数が導入されます。θabは、固定子位相巻線aに対する使用される固定参照フレームの位置を決定します。

3つの位相量は次の式を使ってαβ成分に変換されます。

$X_{αβo} = T_{ABC / αβo} {٠ X}_{ABC}$

ここで、X は電圧、電流、または磁束のベクトルを表します。

電気変数の定常αβ成分は、次の形式の逆クラーク変換行列を使用して位相値に変換されます。

$T_{αβo / ABC} = [\begin{matrix} c o s θ_{1つの b} & - s 私 n θ_{1つの b} & 1 \\ c o s (θ_{1つの b} - \frac{2 π}{3}) & - s 私 n (θ_{1つの b} - \frac{2 π}{3}) & 1 \\ c o s (θ_{1つの b} + \frac{2 π}{3}) & - s 私 n (θ_{1つの b} + \frac{2 π}{3}) & 1 \end{matrix} \begin{matrix} \end{matrix} \begin{matrix} \end{matrix}]$

3つの位相量のαβ成分は次の式を使用して位相成分に変換されます。

$X_{ABC} = T_{αβo / ABC} ٠ X_{αβo}$

ここで、X は電圧、電流、または磁束のベクトルを表します。

n相機械のαβ変換行列の一般的な形は次のように与えられます。

$T_{ABC / αβo} = \frac{2}{n} [\begin{matrix} c o s θ_{1つの b} & c o s (θ_{1つの b} - \frac{2 π}{n}) & c o s (θ_{1つの b} - \frac{2 ٠ 2 π}{n}) & c o s (θ_{1つの b} - \frac{3 ٠ 2 π}{n}) & ٠ ٠ ٠ & c o s (θ_{1つの b} - \frac{(n - 3) ٠ 2 π}{n}) & c o s (θ_{1つの b} - \frac{(n - 2) ٠ 2 π}{n}) & c o s (θ_{1つの b} - \frac{(n - 1) ٠ 2 π}{n}) \\ - s 私 n θ_{1つの b} & - s 私 n (θ_{1つの b} - \frac{2 π}{n}) & - s 私 n (θ_{1つの b} - \frac{2 ٠ 2 π}{n}) & - s 私 n (θ_{1つの b} - \frac{3 ٠ 2 π}{n}) & ٠ ٠ ٠ & - s 私 n (θ_{1つの b} - \frac{(n - 3) ٠ 2 π}{n}) & - s 私 n (θ_{1つの b} - \frac{(n - 2) ٠ 2 π}{n}) & - s 私 n (θ_{1つの b} - \frac{(n - 1) ٠ 2 π}{n}) \\ c o s θ_{1つの b} & c o s (θ_{1つの b} - \frac{2 ٠ 2 π}{n}) & c o s (θ_{1つの b} - \frac{4 ٠ 2 π}{n}) & c o s (θ_{1つの b} - \frac{6 ٠ 2 π}{n}) & ٠ ٠ ٠ & c o s (θ_{1つの b} - \frac{2 ٠ (n - 3) ٠ 2 π}{n}) & c o s (θ_{1つの b} - \frac{2 ٠ (n - 2) ٠ 2 π}{n}) & c o s (θ_{1つの b} - \frac{2 ٠ (n - 1) ٠ 2 π}{n}) \\ - s 私 n θ_{1つの b} & - s 私 n (θ_{1つの b} - \frac{2 ٠ 2 π}{n}) & - s 私 n (θ_{1つの b} - \frac{4 ٠ 2 π}{n}) & - s 私 n (θ_{1つの b} - \frac{6 ٠ 2 π}{n}) & ٠ ٠ ٠ & - s 私 n (θ_{1つの b} - \frac{2 ٠ (n - 3) ٠ 2 π}{n}) & - s 私 n (θ_{1つの b} - \frac{2 ٠ (n - 2) ٠ 2 π}{n}) & - s 私 n (θ_{1つの b} - \frac{2 ٠ (n - 1) ٠ 2 π}{n}) \\ c o s θ_{1つの b} & c o s (θ_{1つの b} - \frac{3 ٠ 2 π}{n}) & c o s (θ_{1つの b} - \frac{6 ٠ 2 π}{n}) & c o s (θ_{1つの b} - \frac{9 ٠ 2 π}{n}) & ٠ ٠ ٠ & c o s (θ_{1つの b} - \frac{3 ٠ (n - 3) ٠ 2 π}{n}) & c o s (θ_{1つの b} - \frac{3 ٠ (n - 2) ٠ 2 π}{n}) & c o s (θ_{1つの b} - \frac{3 ٠ (n - 1) ٠ 2 π}{n}) \\ - s 私 n θ_{1つの b} & - s 私 n (θ_{1つの b} - \frac{3 ٠ 2 π}{n}) & - s 私 n (θ_{1つの b} - \frac{6 ٠ 2 π}{n}) & - s 私 n (θ_{1つの b} - \frac{9 ٠ 2 π}{n}) & ٠ ٠ ٠ & - s 私 n (θ_{1つの b} - \frac{3 ٠ (n - 3) ٠ 2 π}{n}) & - s 私 n (θ_{1つの b} - \frac{3 ٠ (n - 2) ٠ 2 π}{n}) & - s 私 n (θ_{1つの b} - \frac{3 ٠ (n - 1) ٠ 2 π}{n}) \\ ٠ ٠ ٠ & ٠ ٠ ٠ & ٠ ٠ ٠ & ٠ ٠ ٠ & ٠ ٠ ٠ & ٠ ٠ ٠ & ٠ ٠ ٠ & ٠ ٠ ٠ \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & ٠ ٠ ٠ & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & - \frac{1}{2} & \frac{1}{2} & - \frac{1}{2} & ٠ ٠ ٠ & - \frac{1}{2} & \frac{1}{2} & - \frac{1}{2} \end{matrix}]$

ここで、n はフェーズの数です。

行列の最初の2行は、基本的な磁束とトルクの発生につながる変数を定義します。最後の2行は2つの零相成分を定義し、変換行列の最後の行は、奇数相数nに対しては省略されます。中間には、偶数相数の場合は(n - 4)/2組の行があり、それぞれ(n - 4)/2組の変数が定義され、奇数相数の場合は(n - 3)/2組の行と変数が定義されます。これらの成分は、特定の電圧、磁束、および電流の高調波に対応しており、トルクの発生には寄与しません。

回転dq参照フレーム

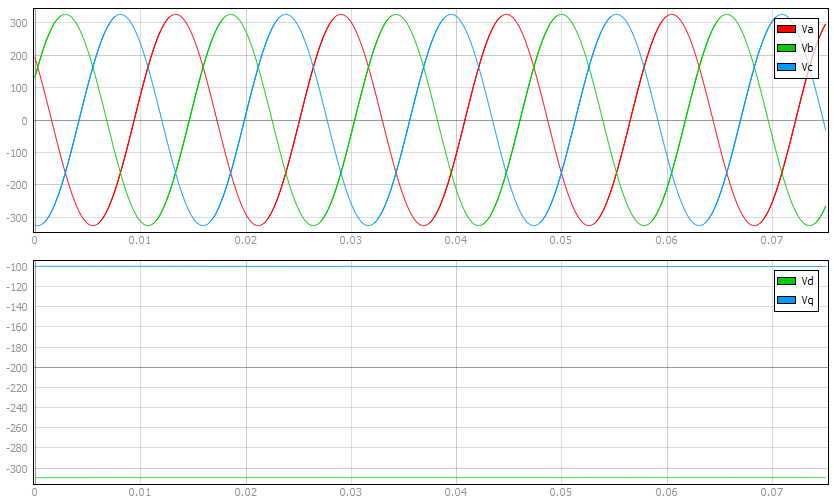
パーク変換は、固定子と回転子の電気変数を元の 3 相領域から回転する 2 相 dq 領域に変換します。

電気変数は、変換行列を使用して dq 成分に変換されます。

$T_{ABC / ドコ} = \frac{2}{3} [\begin{matrix} c o s (ω t + θ_{1つの b}) & c o s (ω t - \frac{2 π}{3} + θ_{1つの b}) & c o s (ω t + \frac{2 π}{3} + θ_{1つの b}) \\ - s 私 n (ω t + θ_{1つの b}) & - s 私 n (ω t - \frac{2 π}{3} + θ_{1つの b}) & - s 私 n (ω t + \frac{2 π}{3} + θ_{1つの b}) \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{matrix}]$

回転フレームの位置は ωt で与えられます。ここで、 ω は dq フレームの回転速度を表します。θabは、固定子相巻線aに対する使用される回転参照フレームの位置を決定します。

3 つの相量は次の式を使用して dq 成分に変換されます。

$X_{ドコ} = T_{ABC / ドコ} ٠ X_{ABC}$

ここで、X は電圧、電流、または磁束のベクトルを表します。

電気変数の回転 dq 成分は、次の形式の逆パーク変換行列を使用して位相値に変換されます。

$T_{ドコ / ABC} = [\begin{matrix} c o s (ω t + θ_{1つの b}) & - s 私 n (ω t + θ_{1つの b}) & 1 \\ c o s (ω t - \frac{2 π}{3} + θ_{1つの b}) & - s 私 n (ω t - \frac{2 π}{3} + θ_{1つの b}) & 1 \\ c o s (ω t + \frac{2 π}{3} + θ_{1つの b}) & - s 私 n (ω t + \frac{2 π}{3} + θ_{1つの b}) & 1 \end{matrix}]$

3 つの位相量の dq 成分は次の式を使用して位相成分に変換されます。

$X_{ABC} = T_{ドコ / ABC} ٠ X_{ドコ}$

ここで、X は電圧、電流、または磁束のベクトルを表します。

マシンライブラリコンポーネントのリスト

Typhoon HIL Schematic Editor の現在のバージョンでは、次のタイプのマシンコンポーネントを選択できます。

参考文献

機械コンポーネントは、次の文献に記載されている原則に基づいて実装されました。

電気機械の解析、ポール・クラウス著、ニューヨーク：マグロウヒル、1986年頃
Paul C. Krause、Oleg Wasynczuk、Scott D. Sudhoff、 「Analysis of Electric Machinery 」、IEEE Press、2002 年。
Liwei Wang、 「電力システムにおける電磁過渡現象のリアクタンス後ろ電圧定式化を使用した AC マシンのモデリング」 、ブリティッシュコロンビア大学、バンクーバー、2010 年。
Robert Vartanian、 「ファンおよびポンプ用途向け永久磁石補助同期リラクタンスマシン (PMa-SynRM) の設計および性能分析」 、テキサス A&M 大学博士論文、2014 年。
Xiao Chen、Jiabin Wang、Bhaskar Sen、Panagiotis Lazari、Tianfu Sun、 「磁気飽和、空間高調波、鉄損効果を考慮した内部永久磁石マシンの高忠実度かつ計算効率の高いモデル」 、IEEE、2015 年。
IM Canay、 「同期機の回転子量の計算における不一致の原因と正確な等価図」 、IEEE、1969 年。
Alberto Berzoy、Ahmed AS Mohamed、Osama Mohammed、 「故障検出および識別のための誘導機のターン間故障の複素ベクトルモデル」 、IEEE、2016。
Liwei Wang、Juri Jatskevich、Steven D. Pekarek、 「リアクタンス背後電圧定式化を使用した誘導機のモデリング」 、IEEE、2008 年。
Emil Levi、Radu Bojoi、F. Profumo、Hamid Toliyat、 「多相誘導モータードライブ - 技術の現状レビュー」 、IET Electric Power Applications、2007 年。